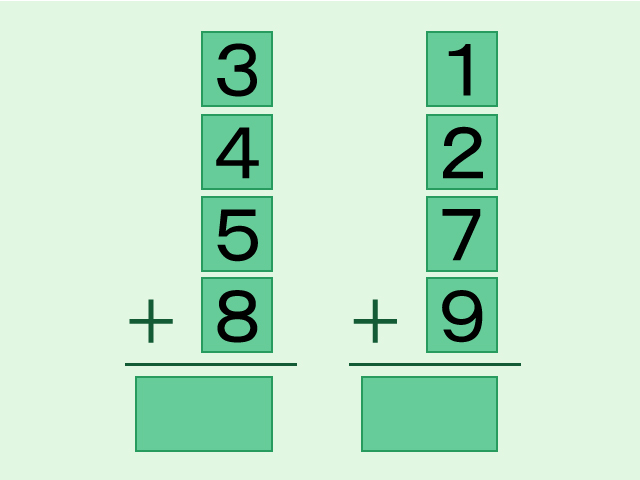
1桁の数が書かれたカードが8枚あります。8枚のカードを4枚ずつに分けて左側と右側の2列に並べました。今の状態では、左側に並んでいる4枚のカードの和と右側に並んでいる4枚のカードの和は異なっています。しかし、左側から1枚、右側から1枚のカードを選んで入れ替えると左右に並んでいるカードの和が等しくなります。あなたは入れ替える2枚のカードを見つけることができるでしょうか。
最初に左右に並んでいるカードの和を確認しましょう。
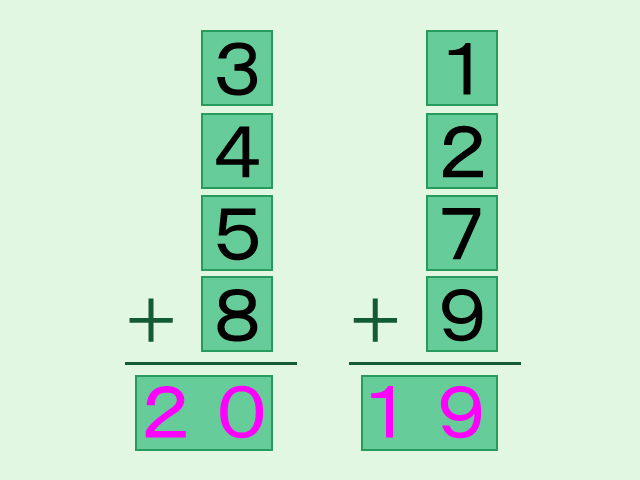
左側に並んでいる4枚のカードの和は20(3+4+5+8=20)です。右側に並んでいる4枚のカードの和は19(1+2+7+9=19)です。確かに、左右の列に並んでいる数の和は異なっています。では、どのカードを入れ替えると、左右の列の和が等しくなるのでしょうか。どのカードを入れ替えたら良いのか見当もつかないというのが正直なところではないでしょうか。
取り合えず、一番上に並んでいる「3」と「1」を入れ替えてみました。左右それぞれの和を確認してみて下さい。
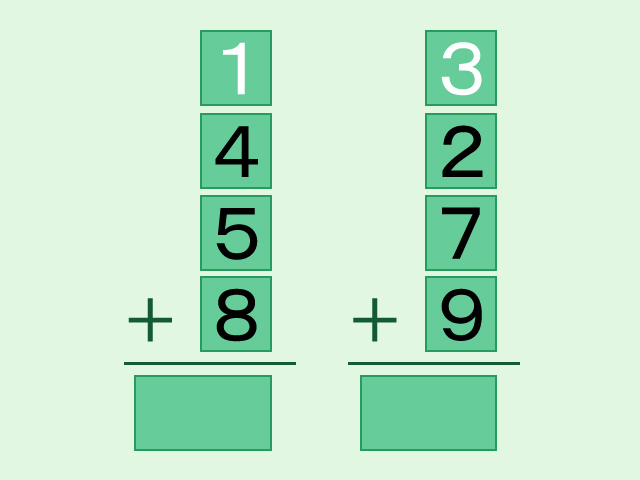
左側の和は「18」で、右側の和は「21」です。依然として左右の和は異なっています。入れ替えるのはこの2枚のカードではないようです。では、次に「8」と「9」のカードを入れ替えてみましょう。
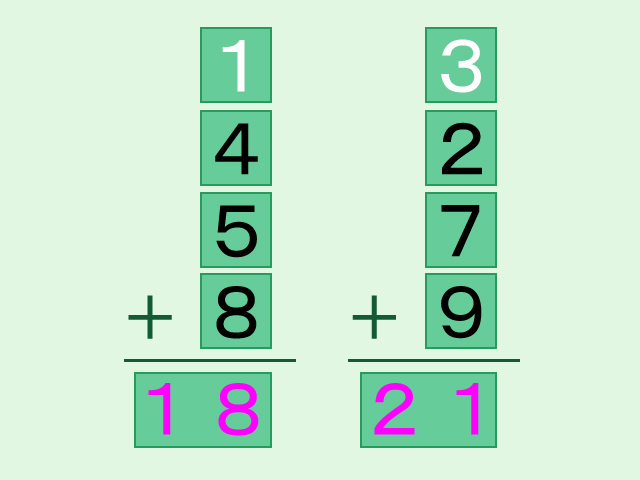
入れ替えた「8」と「9」のカードの文字を、今度はオレンジ色にしています。「3」と「1」のカードはもとの場所に戻しました。この状態で左右の和を求めてみて下さい。
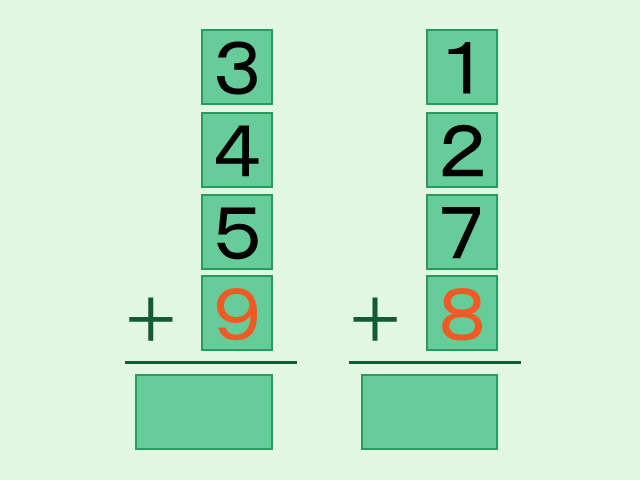
左側の和は「21」で、右側の和は「18」です。やはり、和は等しくなりませんね。もうお気づきの人もいるかと思いますが、どのようにカードを入れ替えても左右の和が等しくなることはありません。
1+2+3+4+5+7+8+9=39となりますから、8個の数の和は39となります。つまり、左右の和が等しくなるのはそれぞれの和が19.5になった時です。整数の和が小数になることはないので、2枚のカードを入れ替えて左右の和が等しくなることはないのです。
しかし、少し工夫をすると左右の和は等しくなるのです。今、左側の和は「21」で、右側の和は「18」です。「21」と「18」の差は「3」です。この「3」という数に大きな意味があるのです。さぁ、あなたはどのような工夫をしますか。「9」と書かれたカードをよく見て下さい。
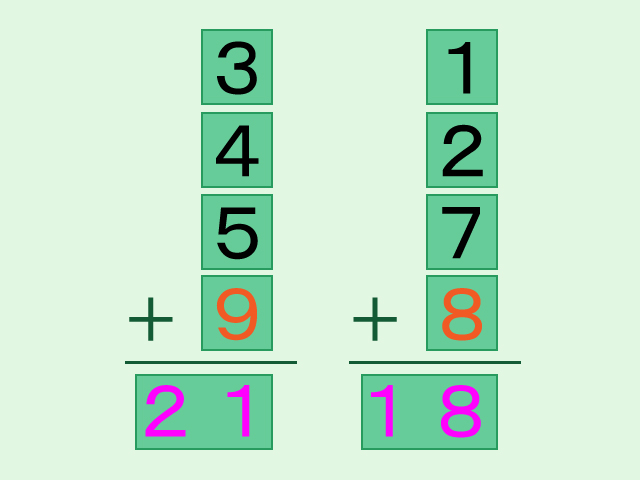
「9」と書かれたカードをひっくり返すと「6」というカードになります。「9」と「6」の差は「3」ですね。左右の和を確認してみましょう。
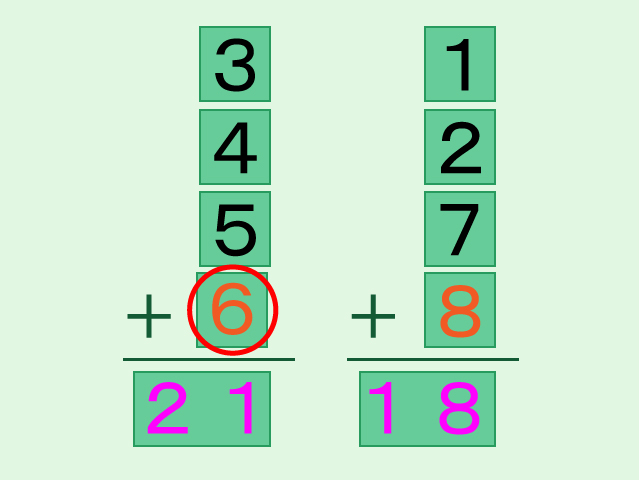
左側の和は「18」です。そして、右側の和も「18」になっています。
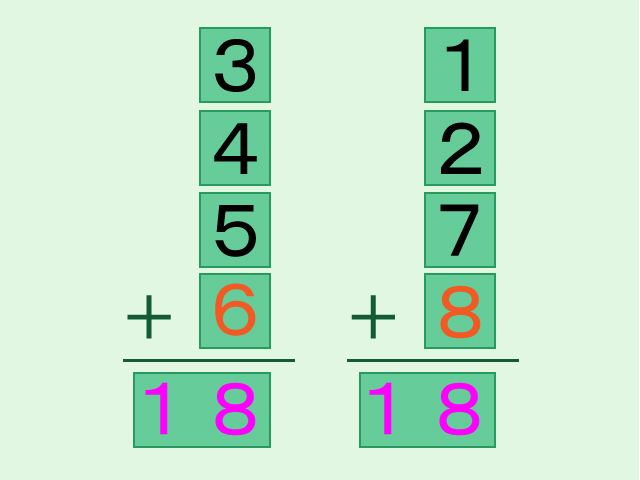
答えです。
左側にある「8」と「9」のカードをを入れ替えて「9」のカードをひっくり返すと、左右の和が等しくなります。もちろん、「9」のカードをひっくり返してから2枚のカードを入れ替えても構いません。
2枚のカードを入れ替えるだけでは和は等しくなりません。カードをひっくり返して新しい数をつくるという柔軟な発想が必要でした。
色々なパズルを解いていくうちに、柔軟な発想ができるようになるかもしれません。「パズルの記事」一覧 もご覧ください。
