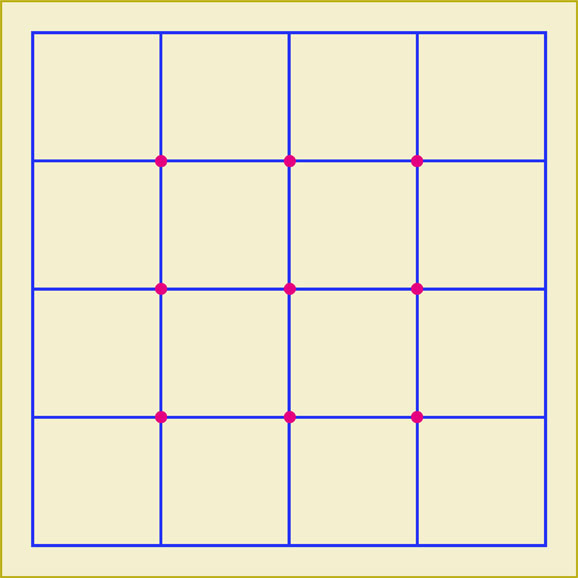
赤い点が上の図のように9個並んでいます。9個の点のうちの4個の点を通る円はいくつ描くことができると思いますか。描くことができる円の総数を答えて下さい。簡単に見つけることができる円もあるのですが、「あっ、こんな4点を通る円も描くことができたんだ。全然気付かなかったよ。」という円もあります。あなたはいくつのの円を見つけ出すことができるでしょうか。
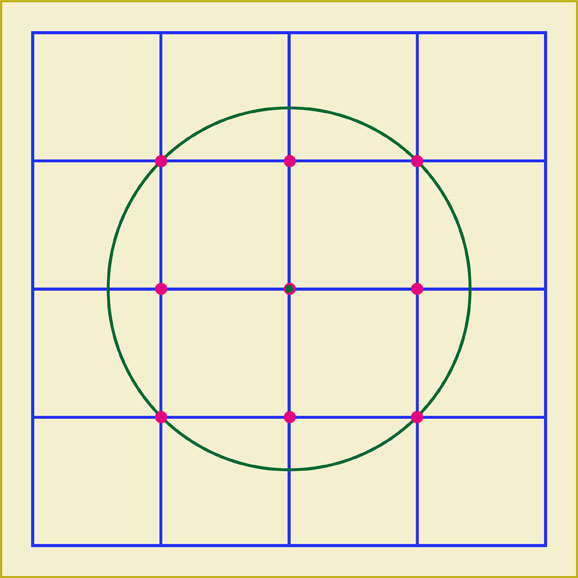
この円は4個の赤い点を通っています。
試しに大きな円を1個描いてみました。円周上には4個の赤い点があります。条件に当てはまっていますね。
他にはどのような円を描くことができるのでしょうか。円を描くためには、円の中心位置を把握することが大切です。円周上の点となる4点が決まると中心の位置も決まります。では、どのようにすると中心の位置がわかるのでしょう。
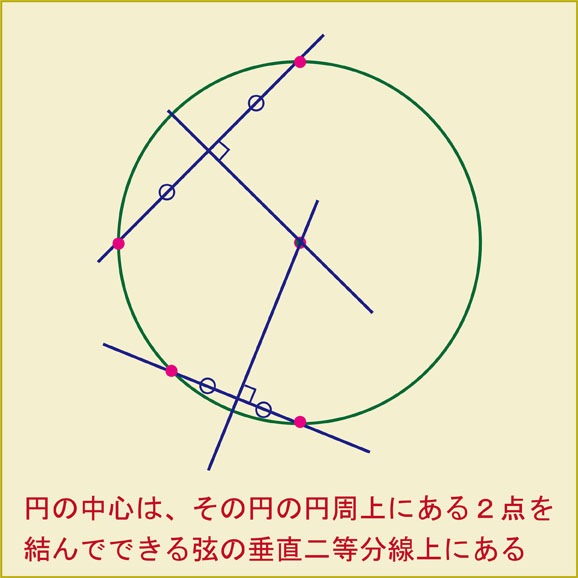
円の中心がある場所
円周上の適当な場所に2個の点を通る直線を引くと弦ができます。円の中心は弦の垂直二等分線上にあることが知られています。しかし、円の中心の位置を特定することはできません。
円の中心の位置を特定するには、2本の弦が必要です。平行ではない2本の弦の交点が円の中心です。このことを頭の中に入れておくと、4個の赤い点を通る円を描きだすことが出るかもしれません。
下のような位置関係にある4点を選んだ時に描くことができる円はいくつあるでしょうか。
このような4点を通る円はいくつ描くことができますか。簡単すぎる質問でしょうか。しかし、注意してください。下の4点は例として挙げているだけですから、他の場所にある4点を通る円を描くこともできますよ。
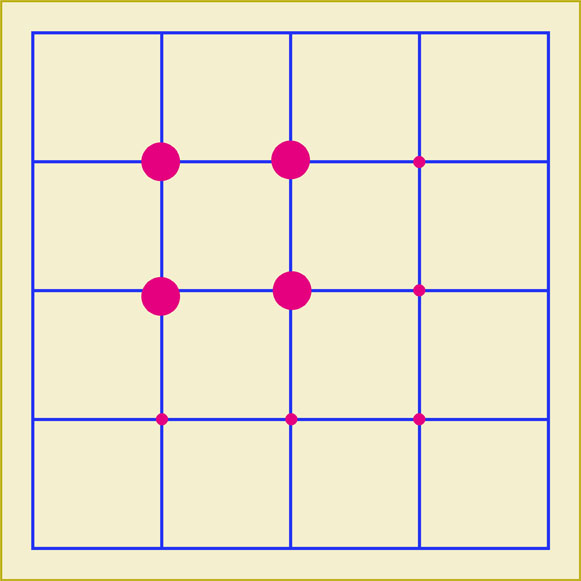
円は4個描くことができました。
上のような位置関係にある4点を選んだ場合、下のように4個の円を描くことができます。円の真ん中に見える小さな点は、それぞれの円の中心です。
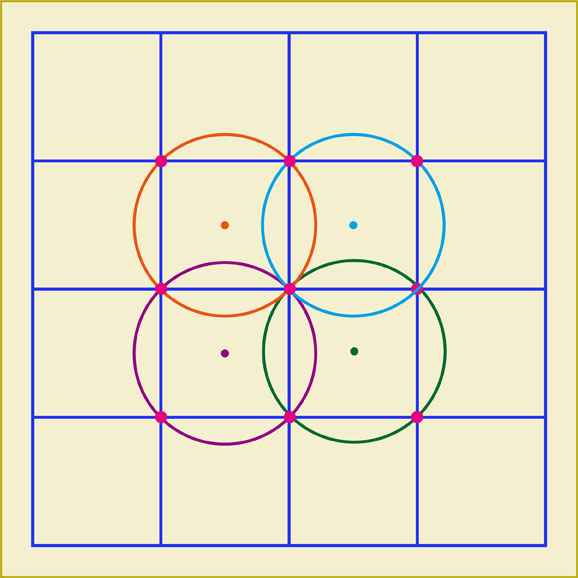
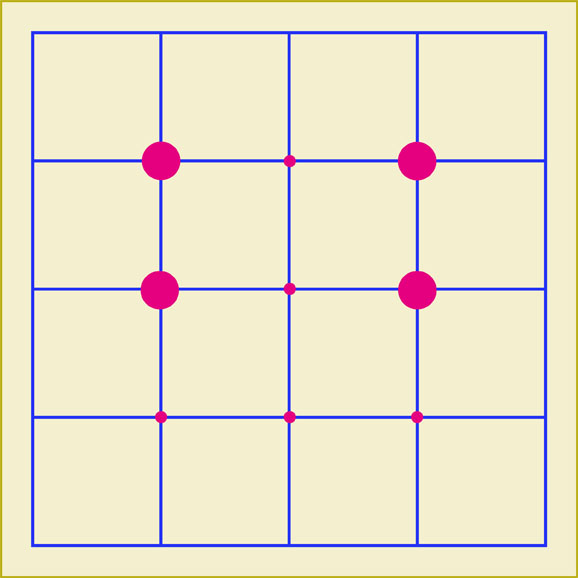
次は下のような位置関係にある4点を選んでみました。
「こんな4点を通る円なんてあるのかな」なんて考えてしまうのではないでしょうか。中心の位置を考えながら円を描いてみて下さい。
円は4個描くことができました。
少し見づらいですが、円は4個描くことができました。円の中心を残しています。
ここまでの円は、割と簡単に描くことができたと思います。しかし、次は少しわかりにくいかもしれません。
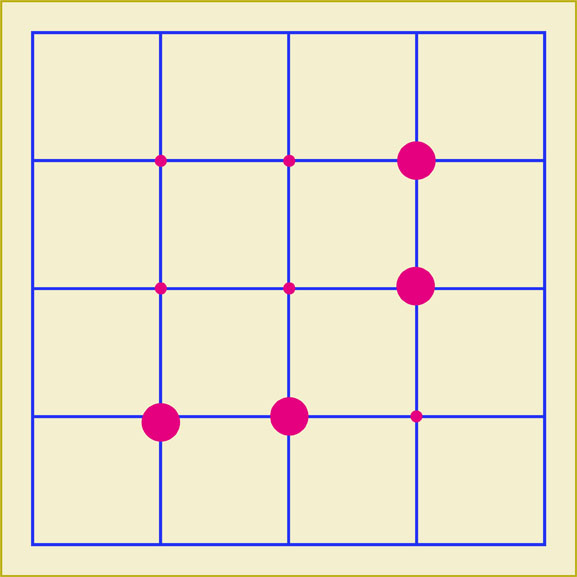
最後は下のような位置関係にある4点を選びました。
このような4点を通る円を描くことができますか。これはちょっとばかり厄介ですね。先ずは円の中心位置を見つけてください。
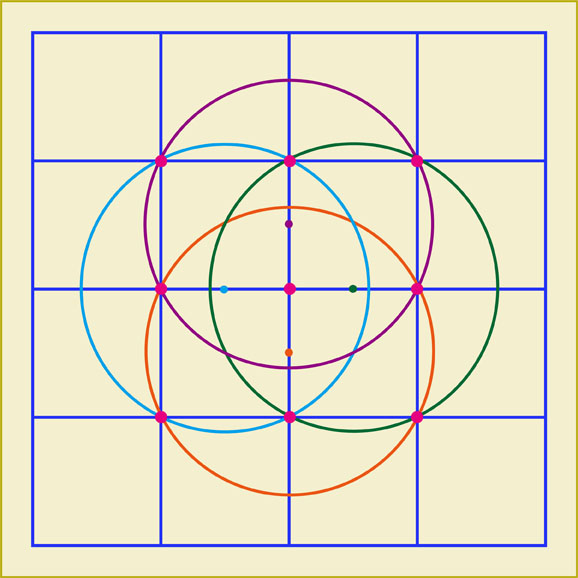
今度は大きな円を4個描くことできました。
円は全部で4個描くことができました。このような位置関係にある4点を通る円を思いつくまでには、少々時間が必要だったのではないでしょうか。
4点を通る円はこれですべてです。全部でいくつになったでしょう。
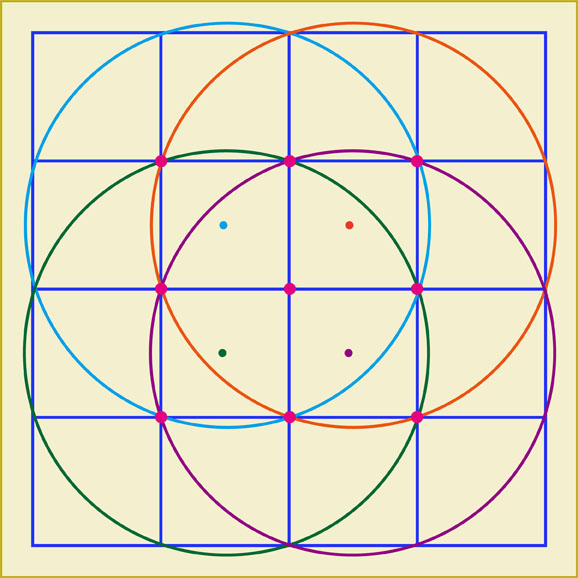
答えです。
9個の赤い点の中の4点を通る円は、下に示すように全部で13個ありました。
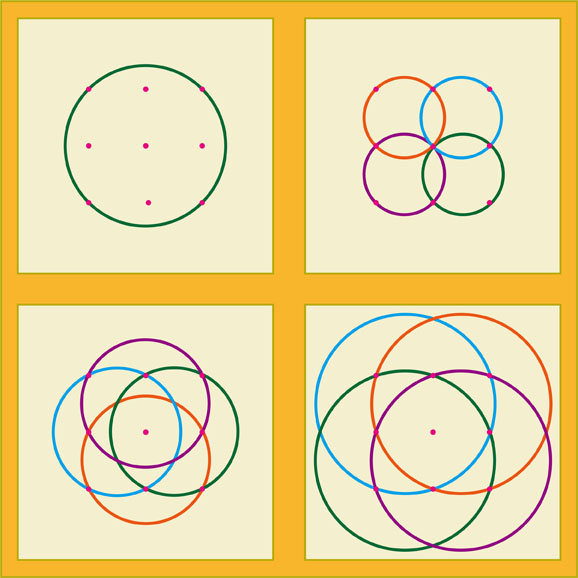
4個の点を通る円が13個もあるなんて想像できたでしょうか。実際に円を描いてみると、円は次々と出てきて驚いてしまったのではないでしょうか。
最後に出てきた大きな円を描くための4点を見つけ出すことができた人は、かなり図形問題に強い人ですね。
図形問題を考えているとあっという間に時間が過ぎていきます。しかし、時間を忘れてしまうほど楽しいのは図形問題だけではありません。大人よりも小学生の方が簡単に答えてしまえるかもしれない数字のパズル のような数字に関する問題にもついついハマってしまいます。
