
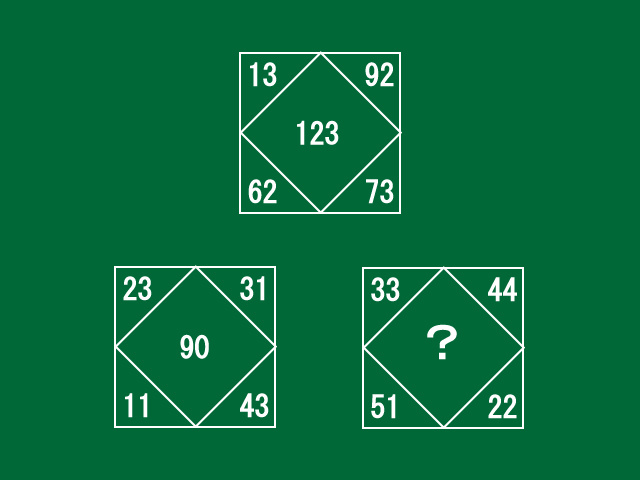
3個の正方形それぞれの中に数字が5個ずつ書かれています。1個の正方形の中に書かれている数字は適当に書かれているわけではなく、ある関係性を持って書かれています。今回の問題は5個の数字の中にある関係性を見つけ出して「?」に適する数字を答えるというものです。この問題を解くには鋭い洞察力を必要とすると思います。しかし、優れた直観力をもっている人は、一瞬で答えを出してしまうのかも知れません。
中央に数字が書かれている正方形を見てみると...。
中央に数字が書かれている正方形で四隅に書かれている数字を見ると、「あっ!」と気付くことがあるのではないでしょうか。向かい合っている数字を見ると、一の位の数字が同じになっています。この関係が残りの正方形についても成り立っていれば、「?」に適する数字を答えることができるかもしれません。
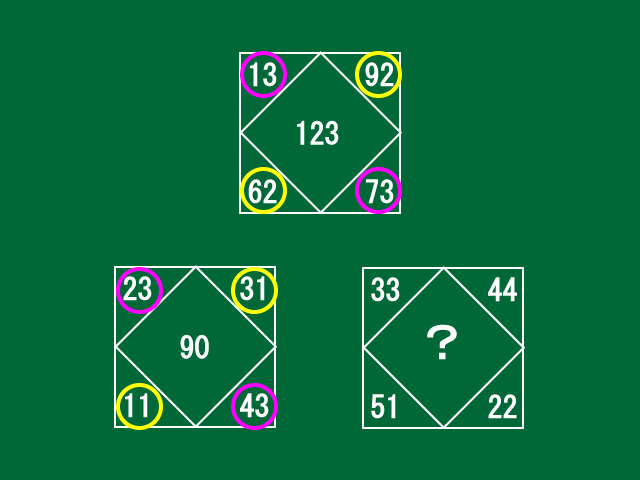
中央が「?」になっている正方形を確認してみましょう。
この正方形に書かれている数字は、他の2個の正方形のような数字の書かれ方はしていないようです。この正方形の中に書かれている数字は、22 → 33 → 44 → 51のように、十の位の数字が1ずつ増えています。
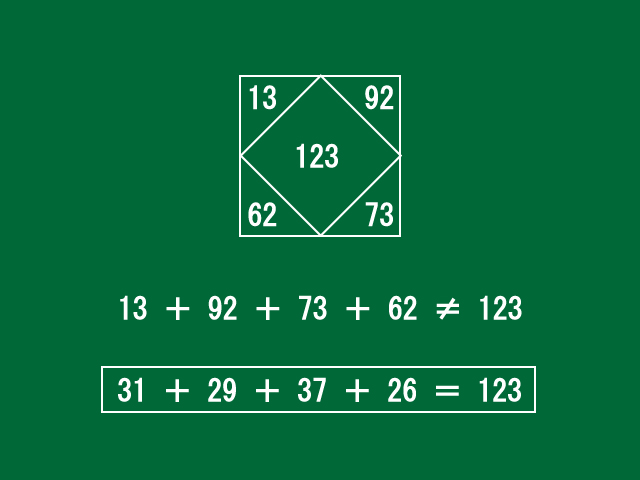
中央の数字が123となっている正方形をもう一度見てみましょう。
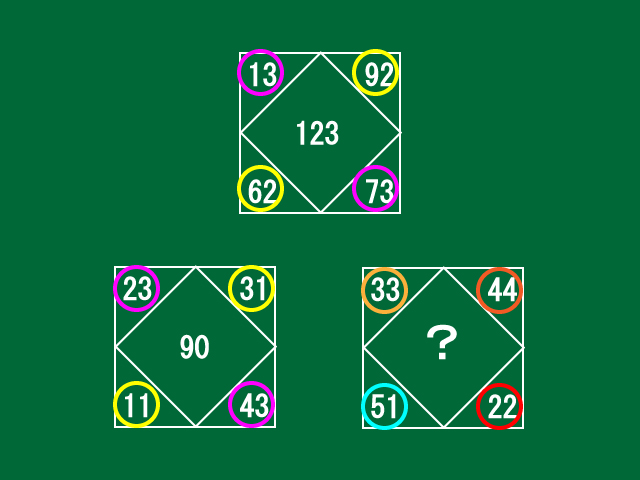
四隅に書かれている数字は、13、92、73、62の4個です。
多分、この4個の数字から、中央に書かれている123という数字ができているのです。4個の数字を足した答えが123ということが考えられますが、4個の数字を足しても123にはなりません。ですから、中央の数字は、四隅の数字を足した答えではありません。
4個の数字を掛けたりすると、123よりも大きな数字になってしまいます。
もう一度4個の数字13、92、73、62を見てみましょう。
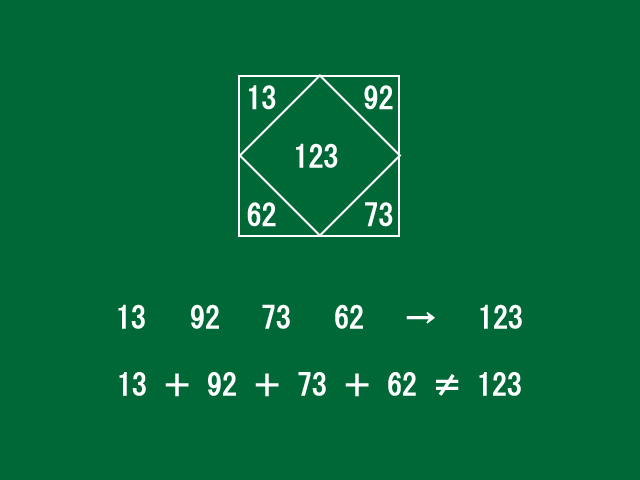
4個の数字を足した答えは123ではありませんでしたが...。
4個の数字で、一の位と十の位の数字を取り替えてみてはどうでしょうか。新しくできる数字は、31、29、37、26です。
31+29+37+26=123になります。123という数字は正方形の中央に書かれている数字と一致しています。これは偶然でしょうか。中央の数字が90になっている正方形でも試してみましょう。
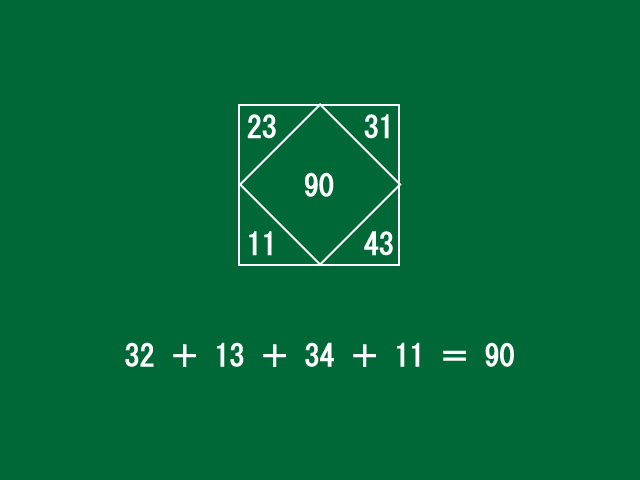
中央の数字が90になっている正方形では...。
四隅の数字で、一の位と十の位の数字を入れ替えてできる数字は、32、13、34、11です。
これらを足した答えは、32+13+34+11=90となります。この90という数字は中央に書かれている数字と一致しています。
ということは...、「?」に適する数字が分かるのではないでしょうか。
「?」に適する数字を求めてみましょう。
四隅に書かれている数字で、一の位と十の位の数字を取り替えてできる数字は、33、44、22、15です。これら4個の数字を足した答えはいくつになるでしょう。

答えです。
「?」に適する数字は114です。
4個の数字を足した答えは、33+44+22+15=114 となります。
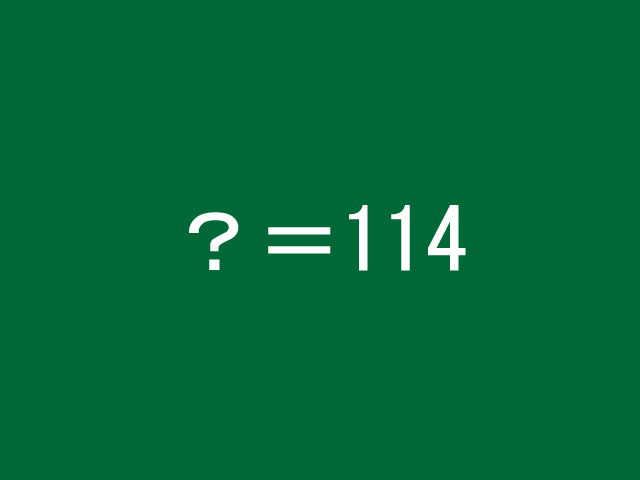
それぞれの正方形の四隅に書かれている数字を、一の位と十の位を取り替えた数字をつくり、それらを足すと中央の数字になるとして、「?」=114という答えを出しました。
しかし、答えはひとつとは限りません。「別の考え方で答えが出たよ!」という方がいらっしゃるかもしれません。
数字に関するパズル、言葉に関するパズルなど、「パズルの記事」一覧 の中には色々な種類のパズルが用意されています。
