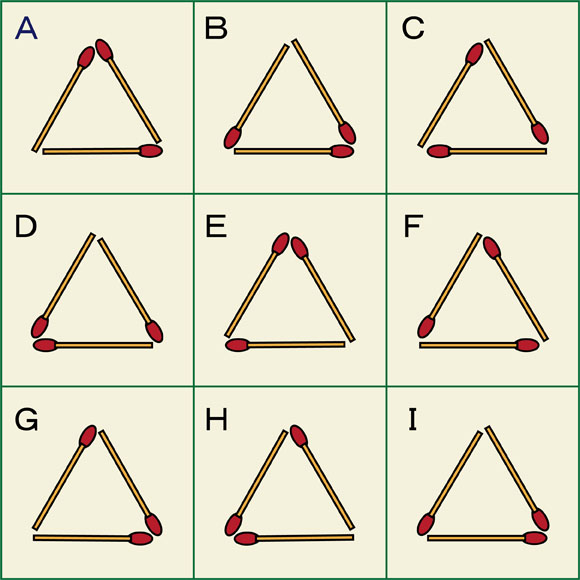
図のようにマッチ棒を3本使って正三角形の形に並べました。それぞれの辺になるマッチ棒の向きを変えることによって、デザイン的に異なる正三角形ができています。ただし、上の9通りの正三角形の中に、デザイン的に一致しているものがあります。それはどの正三角形でしょうか。集中力や注意力が高い人は一瞬のうちに答えを見つけてしまうかもしれません。
デザイン的に一致するとは...。
この問題では、「デザイン的に一致する」ということを次のように考えてください。
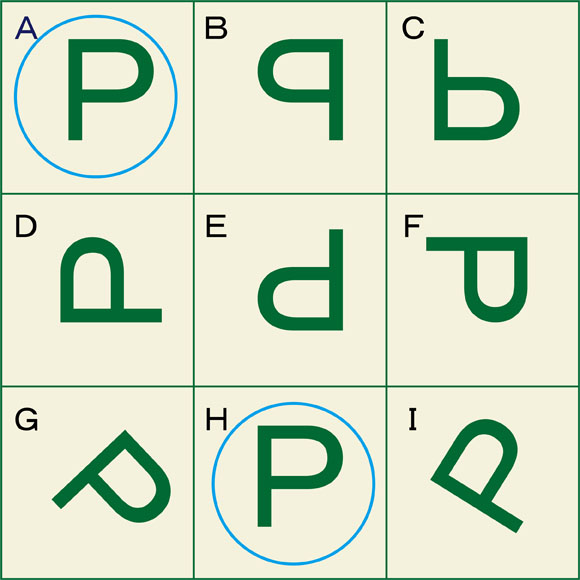
下の図では、アルファベットの「P」の大文字が描かれています。もともとの文字を回転させたり対象移動させたりしています。文字的に見ると、どれもアルファベットの「P」であり同じものと考えられますが、デザインとして見るとAとBに描かれている文字「P」は異なっています。そして、デザインとして一致しているのはAとHに描かれている文字「P」だと考えることができます。
このような考え方で、AからIの正三角形の中から一致している正三角形を探し出してください。
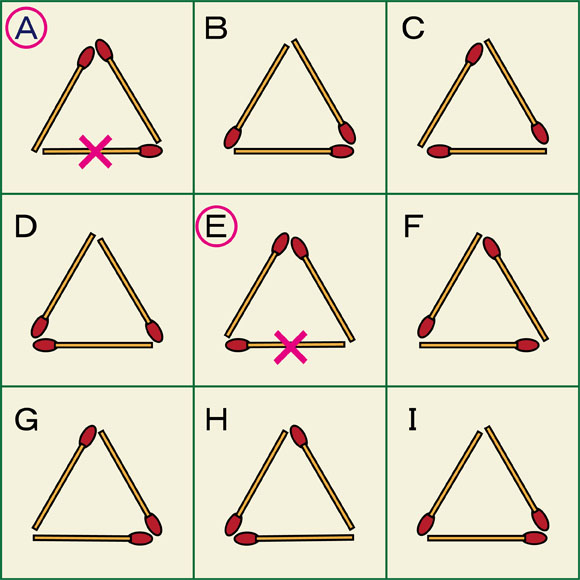
AとEの正三角形が一致しているように見えます。
AとEの正三角形が一致しているように見えますが、実際には一致していません。頂点の部分でマッチ棒の頭が並んでいるという点では一致しています。しかし、底辺の部分を見るとマッチ棒の向きが反対になっています。
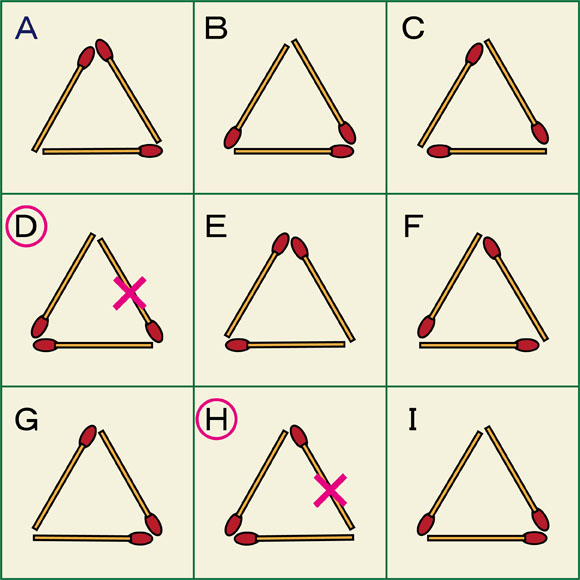
DとHの正三角形でしょうか。
この2つの正三角形も、マッチ棒の頭が並んでいる場所は一致していますが、残りの1本の向きが異なっています。
では、どれとどれが一致しているのでしょうか。
答えです。
デザインとして見る時に一致しているのはBとIの正三角形です。
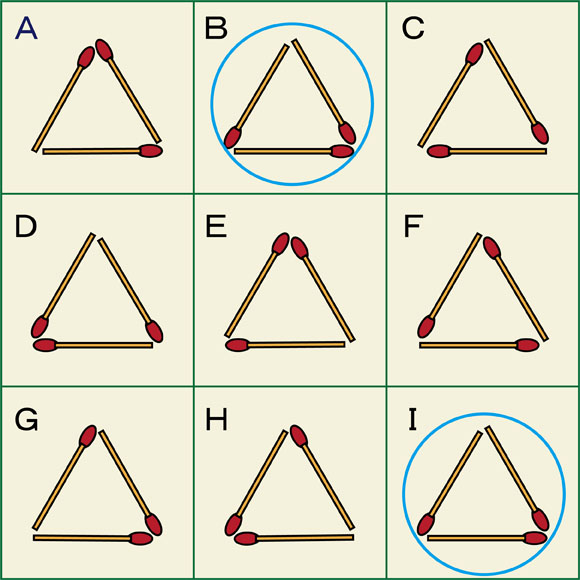
自分では注意深く見ているつもりでも、似たようなものがたくさんあるとすぐに見つけ出すのはなかなか難しいのではないでしょうか。しかし、集中力や注意力が高い人はきっと即答できてしまったのではないでしょうか。
マッチ棒を使ったパズルには、図形パズルや計算式のパズルなど色々な種類があります。マッチ棒を2本移動して正しい式にする という計算式のパズルも、簡単ではありませんでした。
