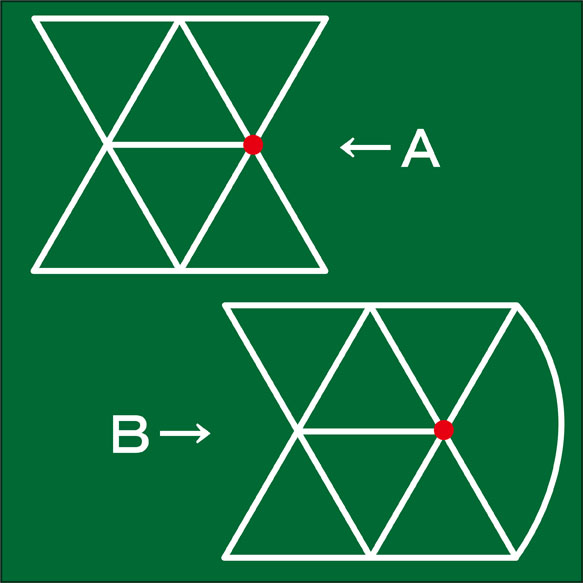
一筆書きの問題です。AとBという2つの図形があるのですが、一筆書きができるのはAとBのうちの一方の図形だけです。どちらが一筆書きができる図形かを答えることができるでしょうか。さらに、答えだと判断した図形で赤丸が一筆書きの始点だとすると、どこが終点の位置になるのかを答えることができるでしょうか。2問合わせて60秒以内で答えられる人は、「一筆書きなら何でもこい!」という人でしょうか。
一筆書きができる図形とできない図形
一筆書きができるかできないかは、実際に書いてみるのが確実のように思われます。確かに、実際に一筆書きができたのであれば、その図形は一筆書きができる図形です。これは間違いありません。
では、実際に書いてみて一筆書きができない図形は、本当に一筆書きができない図形と判断しても構わないでしょうか。もしかしたら、ただ単に書くことができなかっただけで、実際には一筆書きができる図形かも知れません。
実は、一筆書きができる図形とそうではない図形を見分ける方法があります。
図形Aを見て下さい。
図形Aには8個の交点があります。どのような図形でも、その図形の中に含まれている交点を探します。
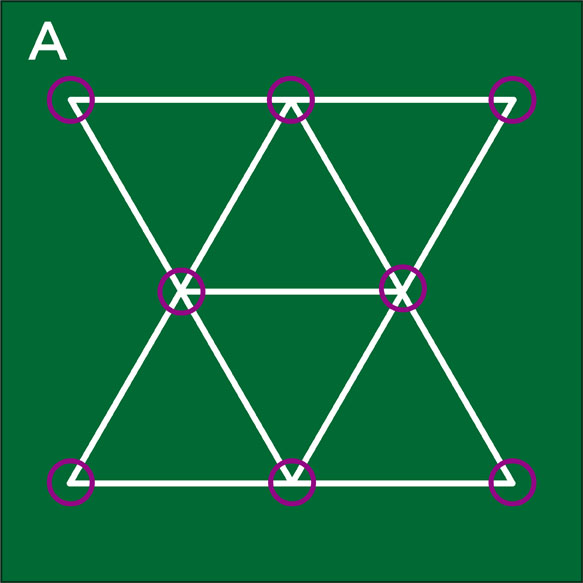
各交点から出ている線の数を確認します。
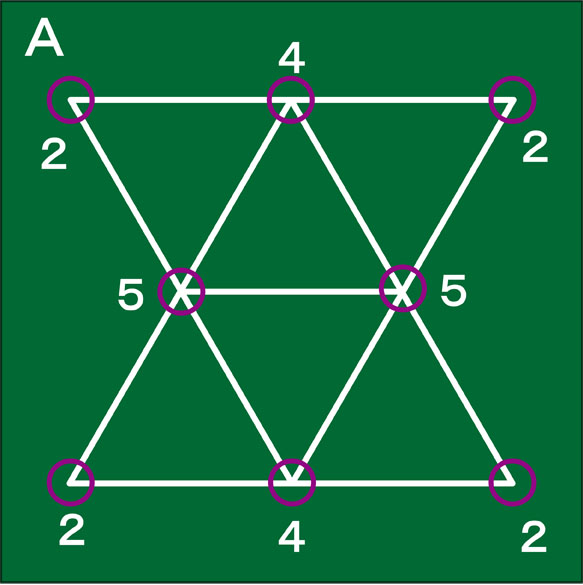
交点を見つけたら、その交点から出ている線(直線や曲線)の数を確認します。図形Aの交点から出ている線の数は下の図のようになっています。
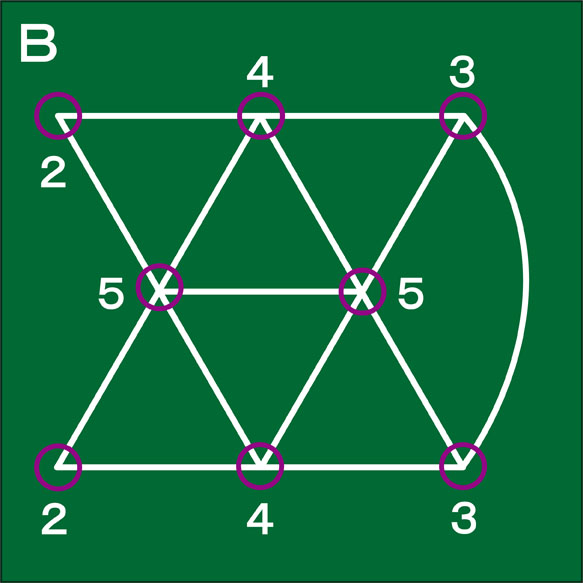
図形Bについて、同じことを調べてみましょう。
図形Bには交点が8個あります。この数は図形Aの交点の数と同じです。
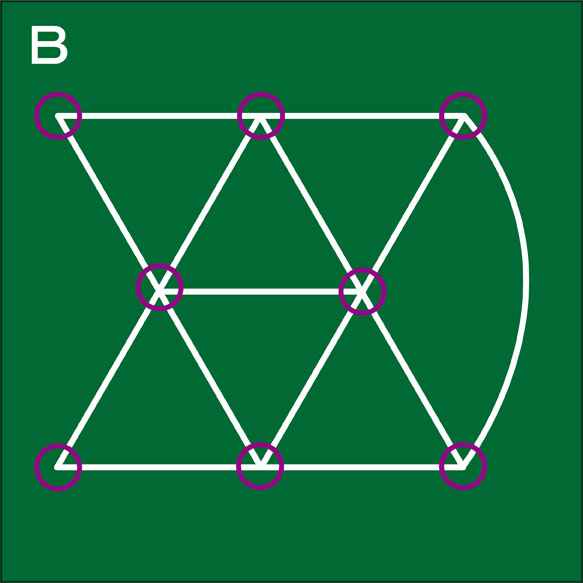
図形Bの各交点から出ている線(直線や曲線)の数は...。
図形Bの各交点から出ている線の数は下の図のようになっています。交点の数は、図形Aも図形Bも変わりありませんが、交点から出ている線の数は異なっています。
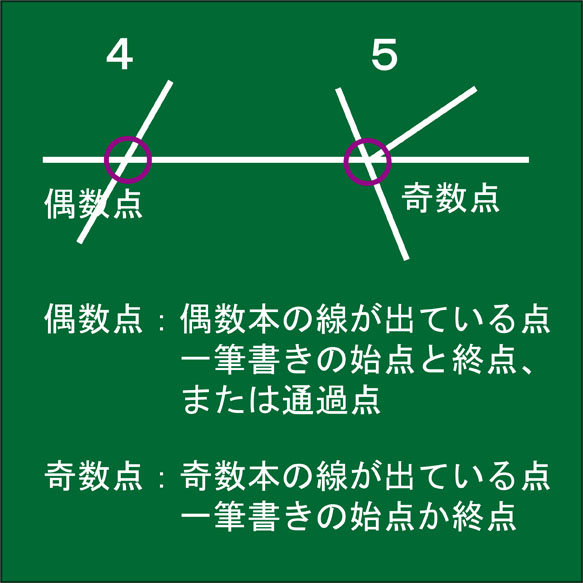
偶数点と奇数点
一筆書きを考えるとき、その図形上にある交点には名前があります。偶数本の線が出ている交点を偶数点(偶点)、奇数本の線が出ている点を奇数点(奇点)といいます。
偶数点は、一筆書きの線が通過していく点です。もし、ひとつの偶数点が一筆書きの始点になっているならば、その点は終点でもあります。
奇数点は、一筆書きをするときの始点か終点になります。偶数点のように始点と終点が一致することはありません。
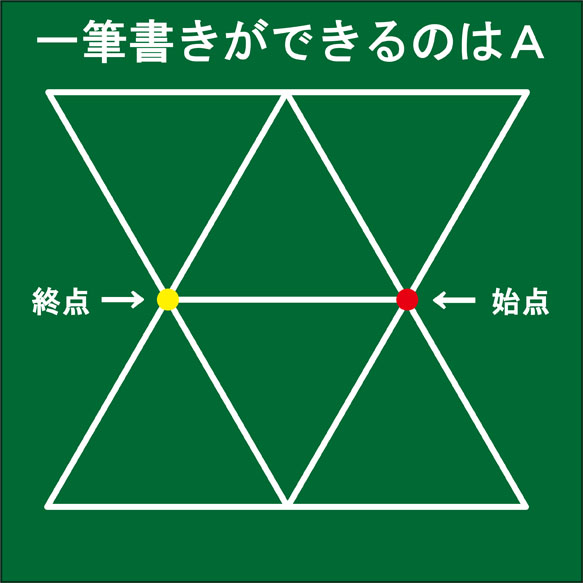
一筆書きができる図形は
交点がすべて偶数点である図形は、どの点を始点にしても一筆書きができ、その点が終点にもなります。また、すべての点が偶数点であるということは、奇数点は0個ということと同じです。
交点の中に奇数点が2個だけである図形も一筆書きができます。奇数点が2個である場合、1個の奇数点が始点となり、もう1個の奇数点が終点となります。奇数点が3個以上ある図形は一筆書きをすることはできません。
以上のことから、一筆書きができる図形と終点を答えることができます。
答えです。
一筆書きができるのは、図形Aの方でした。そして、赤丸を始点とするとき、終点は黄色い丸で示した部分です。赤丸と黄色い丸の部分は奇数点ですから、一筆書きの始点と終点になります。始点と終点は決まっていますが、一筆書きの書き方は何通りもあります。
非常に頭を悩ませる一筆書きの問題もありますが、これからはもう頭を悩ませなくても良いかもしれません。一筆書きの問題は解いてみるだけではなく、作ってみるのも面白いかもしれません。
一筆書きの仕組みがわかってしまったので、瞬時に判れば天才!一筆書きの終点を答える問題! の答えは一瞬で出てしまうかもしれません。



 大谷翔平・野球ニュース
大谷翔平・野球ニュース