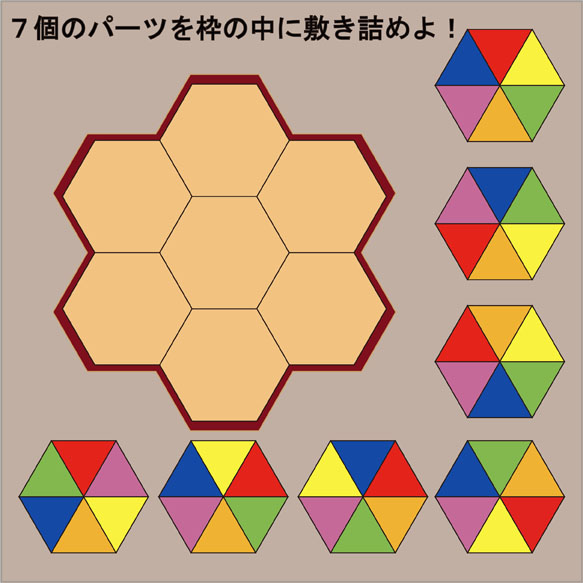
左上に示された枠の中に、周りにある7個のパーツを敷き詰める問題です。パーツを敷き詰めるための条件があります。それぞれのパーツは正六角形の形をしていて、それは異なった色の6個の正三角形で作られています。正六角形を並べるときに、接する辺で作られている正三角形同士の色は同じでなければなりません。7個すべての正六角形について、その条件を満たすように敷き詰めてください。
7個のパーツの特徴
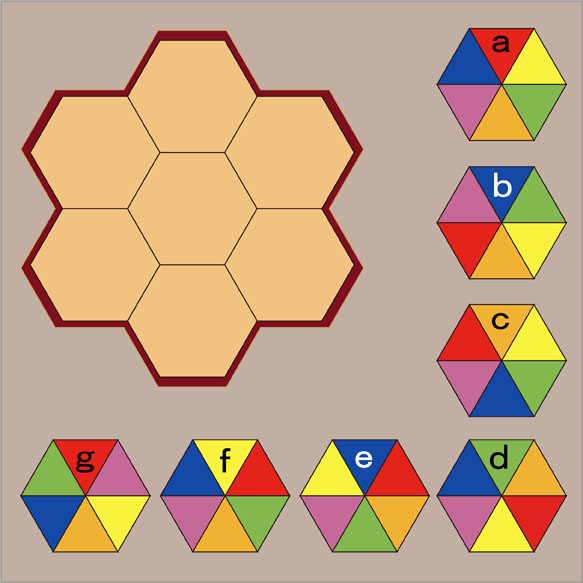
7個のパーツにa、b、c、d、e、f、gという記号を付けました。それぞれのパーツは6色に塗り分けられた6個の正三角形で作られていますが、塗られている色の順序は異なっています。パーツを敷き詰めるときに、それぞれのパーツは回転しても良いですが裏返しにしてはいけません。
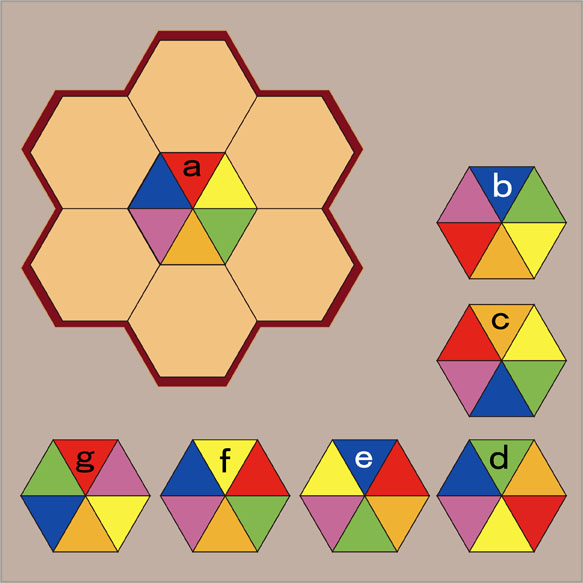
中央に置くパーツは...
中央に置くのはパーツaです。パーツaを置いてしまうとあとは簡単そうですが、それほど簡単ではありません。正六角形の隣り同士の辺でできている正三角形の色が同じであるという条件があります。パーツを置くときに、少し先のことも考えながら置いていくことが必要です。
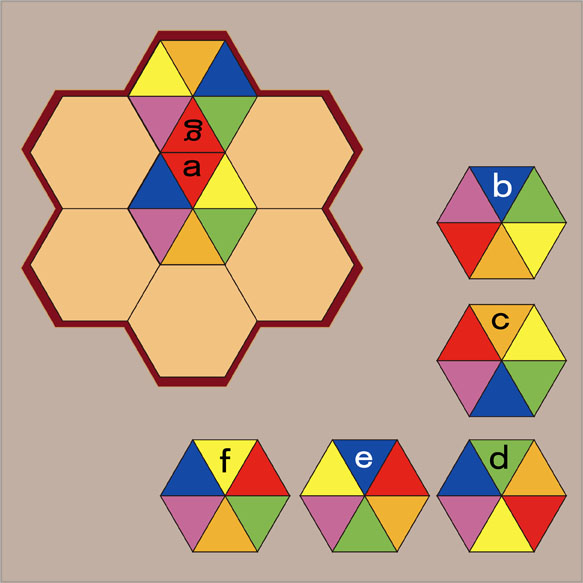
最初に置くパーツは...
最初にパーツgを置いてみましょう。2つの正六角形が枠の中に収まっていて、隣同士になっている正三角形の色も赤色で同じ色になっています。
次に、パーツgの左側に置くパーツを決めましょう。次に置くパーツは、パーツgの紫色の正三角形とパーツaの紺色の正三角形をもつパーツです。
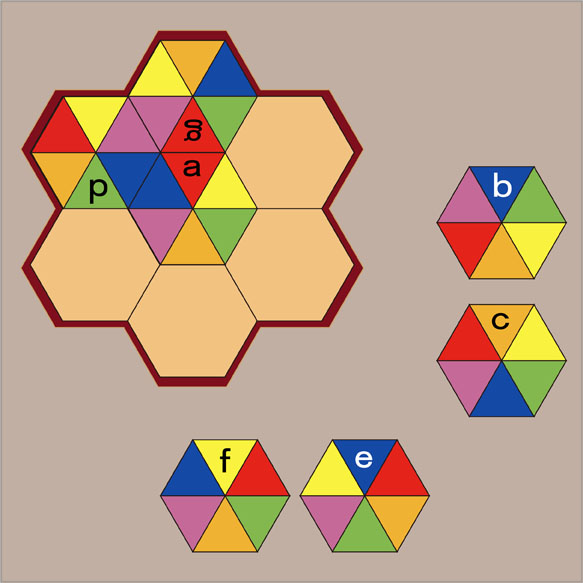
2番目に置くパーツは...
2番目に置くパーツは、紫色の正三角形と紺色の正三角形が隣り合っているパーツです。パーツb、パーツd、パーツfがその条件を満たしていますが、パーツbとパーツfは、実際に置いてみると、最後までパーツを置いていくことができないことがわかります。
つまり、2番目に置くのはパーツdということになります。ただし、パーツdはこのままでは置くことができないので、180°回転させます。
では次に、3番目に置くパーツを考えましょう。3番目に置くパーツは、緑色と紫色の正三角形が隣同士になっているパーツです。
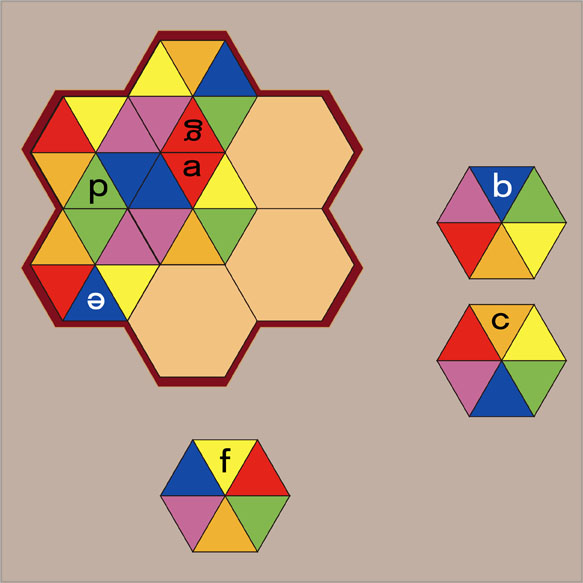
3番目に置くパーツは...
3番目に置くパーツは、緑色と紫色の正三角形が隣同士になっているパーツです。そのようなパーツは、パーツe1個だけです。パーツeを180°回転すると置くことができます。ここまでは順調に置くことができました。残っているパーツは3個です。この3個のパーツで枠を敷き詰めることはできるでしょうか。
4番目に置くパーツを考えてみましょう。4番目に置くパーツは、黄色とオレンジ色の三角形が並んでいるパーツです。
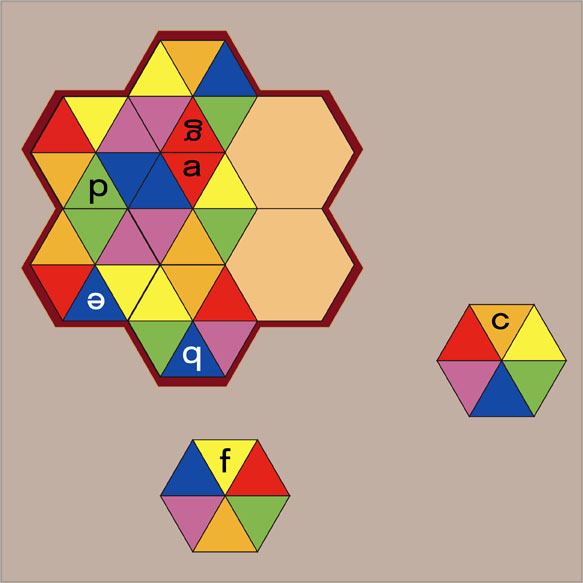
4番目に置くパーツは...
黄色とオレンジ色の三角形が並んでいるパーツは2個ありますが、4番目に置けるのはパーツbです。パーツbを180°回転すると置くことができます。
残っているパーツは2個です。もうお分かりですね。
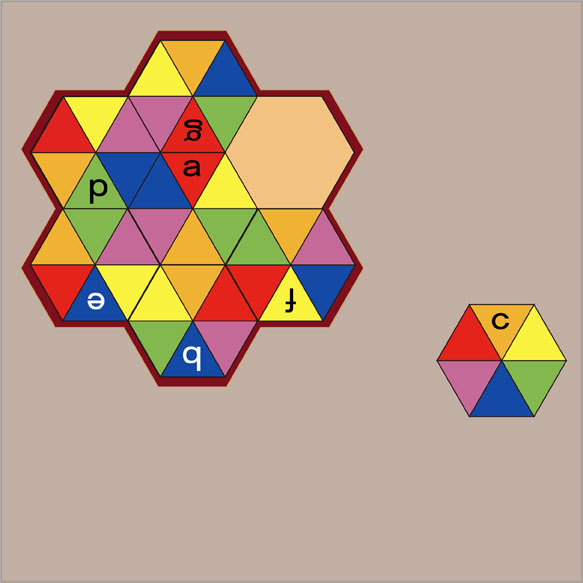
5番目に置くパーツは...
5番目に置いたのは、パーツfです。こちらも回転させています。さて、残っているパーツcは、枠の中に入れることができるでしょうか。
答えです
すべてのパーツが、条件をクリアして枠の中にきれいに収まりました。
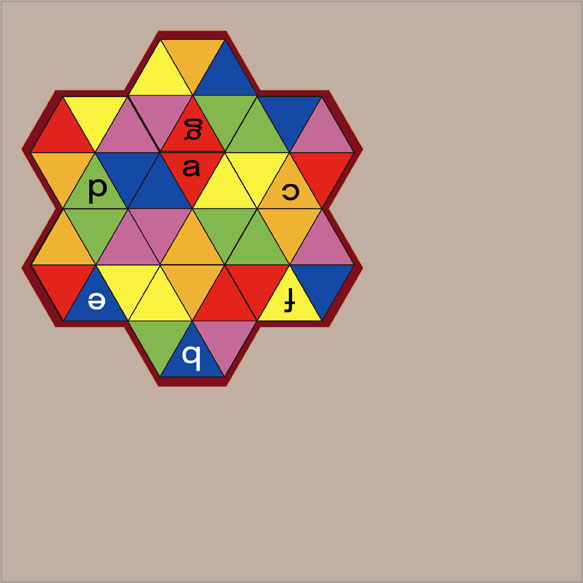
あなたの答えがこの図と異なっていても、回転して同じになれば同じ答えだと考えてください。
a、b、c、d、e、f、gの記号を取ってみましょう。
a、b、c、d、e、f、gの記号をとると、すっきりとして見やすい図形になりました。7個の正六角形が、各辺の隣り同士の正三角形の色が同じになるように並んでいるのがわかります。

正六角形の境目の線を消すとどうなるでしょう
正六角形の境目の線を消すと、今までとは全く別の図形が現れます。これは今回の問題とは関係ありません。おまけの画像です。

今まで平面図形だったのに、なんだか立体図形のように見えている人はいませんか。不思議ですか、立体図形に見える人もいるし、見えない人もいます。
難しいパズルを解いた後は、とんでもない秘密が隠されているはしっこ弁当を見てみませんか。
