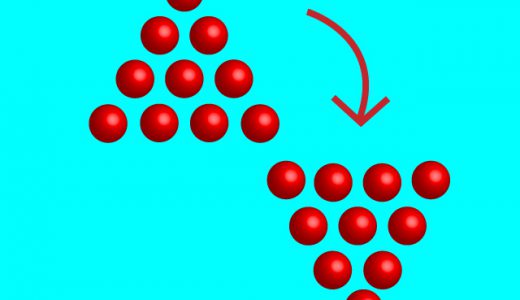
10個の球を図のように上を向いている正三角形の形に並べました。3個の球を移動すると、上向きの正三角形の形をを下向きに変えることができます。簡単そうに見えて、意外と考えさせられる問題です。あなたは簡単い解くことができるでしょうか。それともしばらく考えてしまうでしょうか。パズルが得意な人は、見た瞬間に答えが浮かんできてしまっているかもしれません。
それぞれの球を見分けやすいように、球に番号をつけました。
では先ず、移動する3個の球を見つけましょう。どの球を移動すると良いのでしょうか。

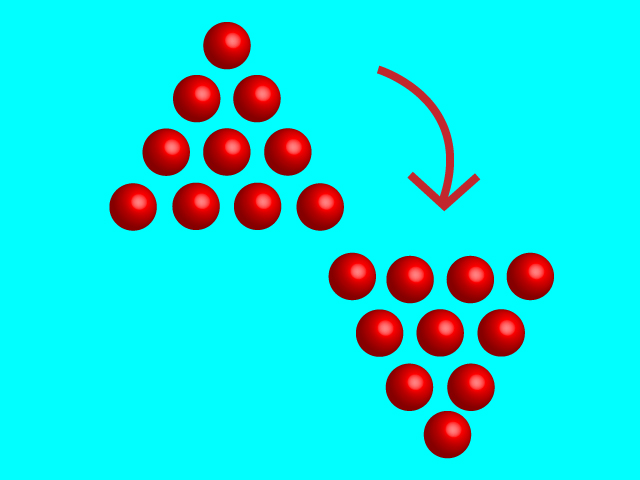
移動する3個の球の色を変えました。
移動するのは、「1」「7」「10」の番号をつけた3個の球です。見やすいように移動する3個の球の色を緑色に変えました。
最初に番号が「1」の球を移動しましょう。あなたなら「1」の球をどこに移動しますか。

「1」の球を、「2」の球の左側に移動しました。
「1」の球の移動先は別にもありますが、今はここに移動して、話を進めていきましょう。
何だか不思議な形になってきました。次に「7」の球を移動しましょう。

「7」の球を右下に移動しました。
「7」の球を右下に移動すると、「10」の移動先が何となく見えてきたのではありませんか。

「10」の球を「3」の球の右隣りに移動しました。
「10」の球を下のように移動すると、上向きだった正三角形が下向きに変わります。
確かに正三角形の向きを変えることができたのですが、自分が考えた答えとは違うと考えている方がいるかもしれません。確かに別の移動法でも下向きの正三角形を作ることができます。

「7」と「10」の球の移動先を交換した場合です。
確かに下向きの正三角形の形が出来上がっています。実は、答となる正三角形の頂点に来る球の番号にこだわるとすると、別の移動方法も考えられます。

「7」の球を「2」の左側に移動させた場合です。
この場合も2通りの移動方法が考えられます。
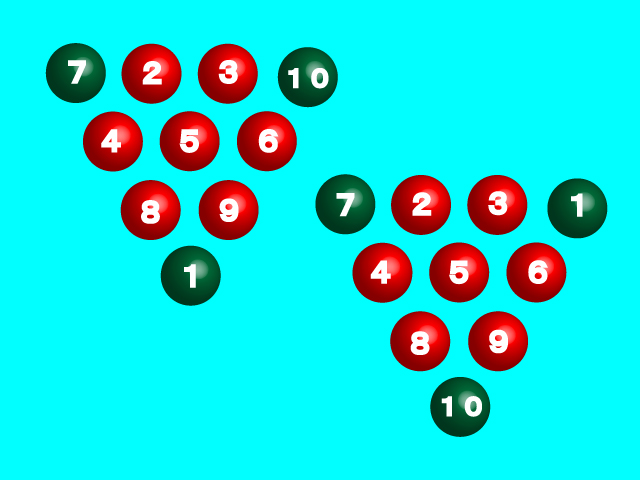
「10」の球を「2」の球の左側に移動させた場合です。
この場合も答えが2通りあります。答えが6通りも出てきてしまいました。
最初の図では番号はついていませんでした。6通りの答えがあるように見えますが、番号は便宜的につけたものでしたから、「どの番号の球をどこに移動したのか」ということは考えなくても良いのです。
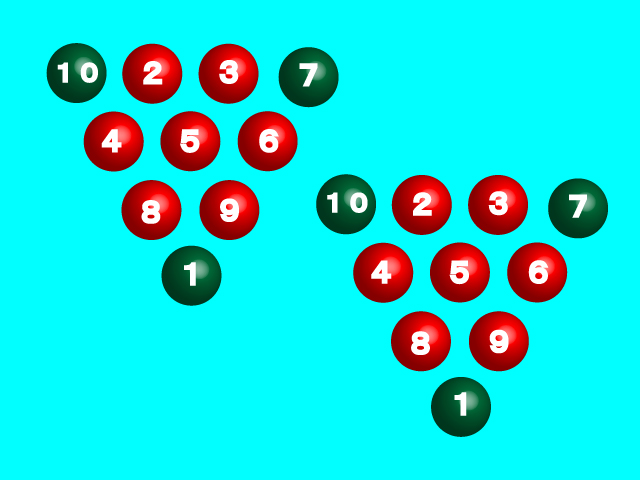
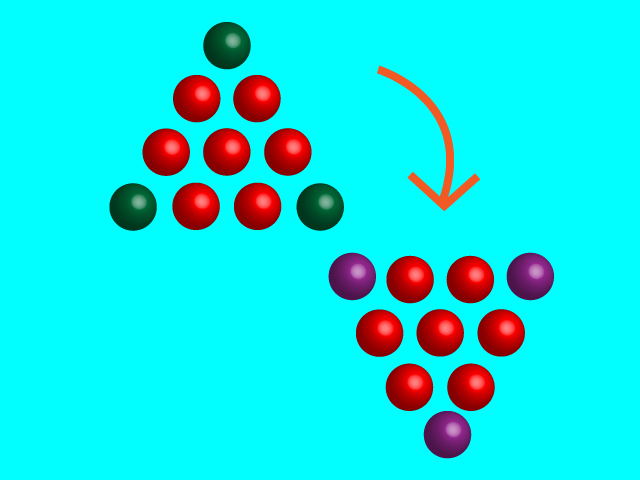
答えです。
問題は移動する3個の球を尋ねていたのですから、緑色にした3個の球を答えると良いことになります。
3か所にある緑色の球を、紫色の球がある場所に移動すれば、下向きの正三角形が出来上がります。どの球をどこに移動するかは自由です。
この問題は、実際に10円硬貨などを並べて考えることもできます。お友達に出題してみてはどうでしょうか。
画面を見ながらひとりで考えるのもよいですが、「パズルの記事」一覧 の中には、お友達と楽しむことができそうな問題もたくさんあります。
