
上に描かれている図形は1本の線でつながっています。つまり一筆書きをすることができる図形です。一筆書きができる図形には、どの点から書き始めてもできる図形と特定の点から書き始めた場合だけにできる図形があります。上の図形は特定の点から書き始めなければ一筆書きをすることはできない図形です。あなたは書き始めの点(始点)を見つけて、一筆書きをすることができるでしょうか。
上の図に描かれている図形を分割しました。
下に描かれている3つの図形は、上で描かれている図形の一部分を取り出したものです。これら3つの図形はすべて一筆書きをすることができます。これら3つの図形を組み合わせてできる図形もまた一筆書きをすることができる図形です。
一筆書きができる図形とできない図形は、実際に書かなくても見分けることができます。どのようにすると見分けることができるのかをご存知ですか。

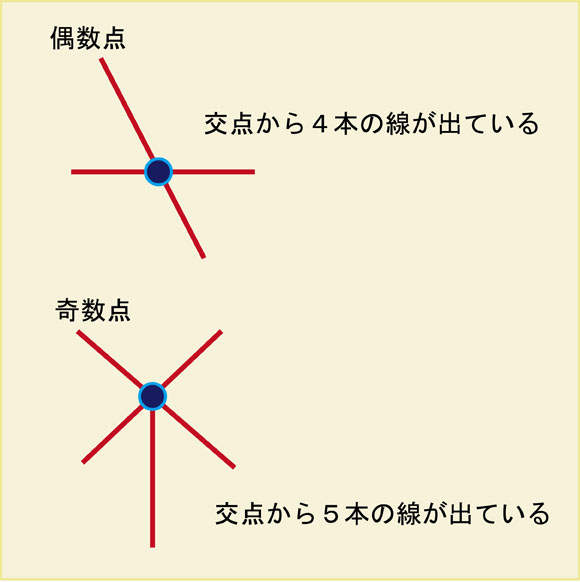
偶数点と奇数点
図形の中にある交点に着目して、交点から出ている線(直線でも曲線でもよい)の数を調べます。交点から出ている線の数が偶数であるとき、その点のことを偶数点または偶点と言います。交点から出ている線の数が奇数であるときは、その点を奇数点または奇点と言います。
偶数点は一筆書きをするときの通過点となります。また、もしこの点から書き始めた場合はその点が書き終わりの点となります。奇数点は通過点とはなりません。書き始めの点か書き終わりの点になります。
以上のことから、一筆書きができる図形はすべての点が偶点であるか、奇数点を2個だけ持っているということがわかります。
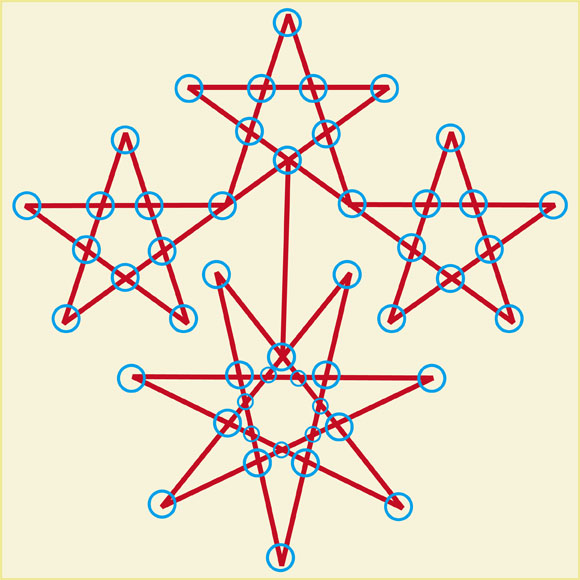
最初に示した図形の中にある点の種類を確認してみましょう。
最初に示した図形の中にある交点に印をつけてみました。これでどの点から書き始めると良いのかがわかるはずです。
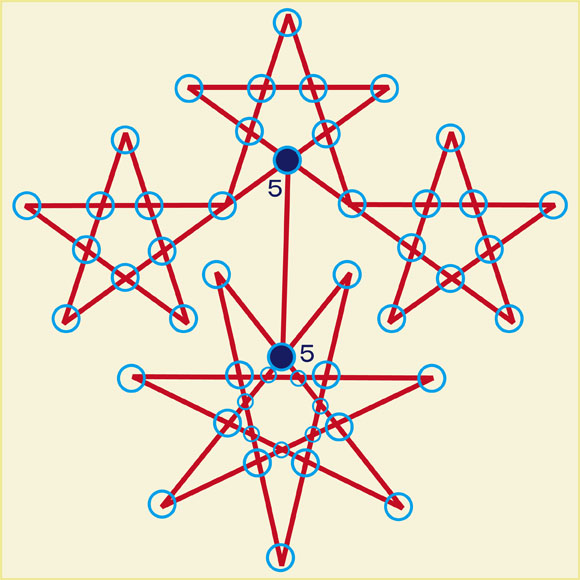
奇数点が2個あります。
全ての点を確認すると、奇数点が2個だけあることがわかります。残りの点はすべて偶数点であることもわかります。紺色の円の部分が奇数点です。それぞれの点から5本の線が出ています。
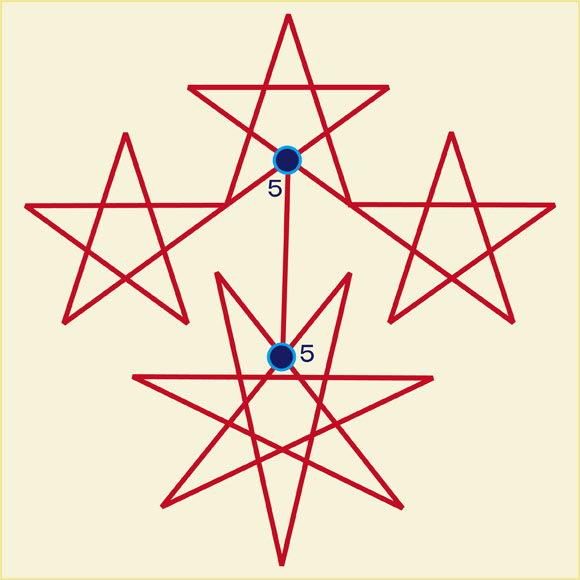
答えです。
2個の奇数点はどちらも書き始めの点とすることができます。2個の奇数点のうちの好きな方から書き始めるともう一方の奇数点で書き終わります。
偶数点と奇数点の個数でわかるのは一筆書きができるかどうかということで、書き方はわかりません。書き方は自分で探さなくてはなりません。
答えの一例です。
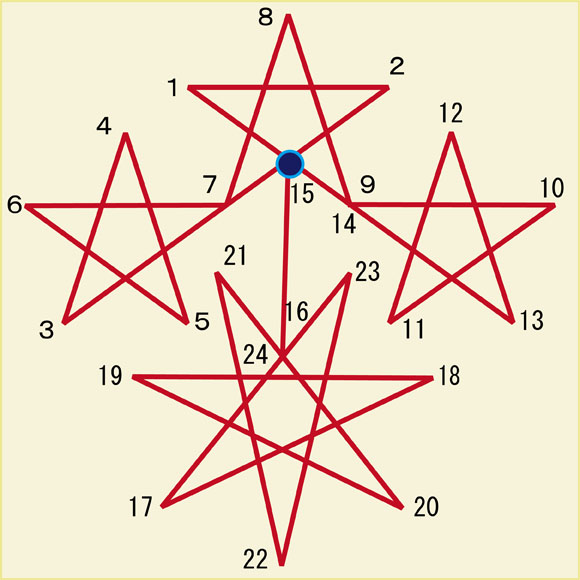
紺色の点から書き始めるとして、その点から1、2、... と順を追って線を結んでいくと、一筆書きができます。これは一例ですから、一筆書きの方法は他にもあります。色々と試してください。
偶数点と奇数点が一筆書きと関係があることがわかると、書き方はわからなくても与えられた図形が一筆書きができるかどうかを判断することができます。
今まで難しいと感じていた一筆書きの問題も、これからは簡単に解くことができるようになったかも知れません。瞬時に判れば天才!一筆書きの終点を答えよ! で一筆書きの問題を考えてみて下さい。
